Trigonometry

Trig packet


Exercises


Trig comp problems

  Introduction  

Radians and degrees

Arc length

Quadrants

  Trigonometric ratios  

Sine, cosine, tangent

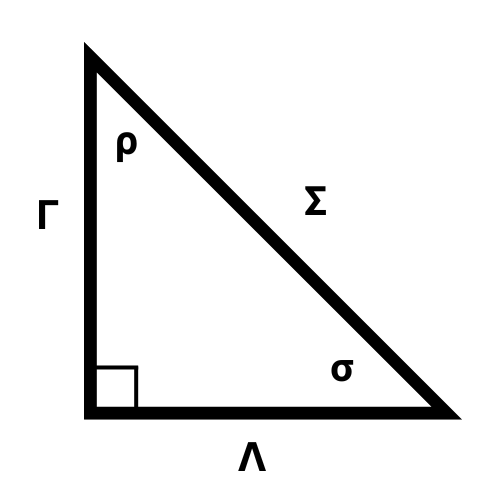
We define the sine of an angle as \begin{equation} \textnormal{Sin} \, (\sigma) = \frac{\Gamma}{\Sigma} \end{equation}

Sine is a ratio of lengths, the length of the opposite side to the hypotenuse.

Similarly, we define the cosine of an angle as \begin{equation} \textnormal{Cos} \, (\sigma) = \frac{\Lambda}{\Sigma} \end{equation}

Cosine is a ratio of the adjacent side to the hypotenuse.

And lastly we have the tangent, which is \begin{equation} \textnormal{Tan} \, (\sigma) = \frac{\Gamma}{\Lambda} \end{equation}

Tangent is a ratio of the opposite side to the adjacent side.

Reciprocal trigonometric ratios

The reciprocal trigonometric ratios are similar to the regular ratios, only that they are the reciprocal.

Cosecant

\begin{equation} \textnormal{Csc} \, (\rho) = \frac{1}{\textnormal{Sin} (\rho)} \end{equation}

Secant

\begin{equation} \textnormal{Sec} \, (\rho) = \frac{1}{\textnormal{Cos} (\rho)} \end{equation}

Cotangent

\begin{equation} \textnormal{Cot} \, (\rho) = \frac{1}{\textnormal{Tan} (\rho)} \end{equation}

  Trigonometry in a right triangle  

Solving a right triangle

Area of right triangle

We find the area of a right triangle with \begin{equation} Area = \frac{1}{2} \, \Lambda \, \Gamma \end{equation} where \( \Lambda \) and \( \Gamma \) are the base and the height.

Special right triangle

  Trigonometry in a general triangle  

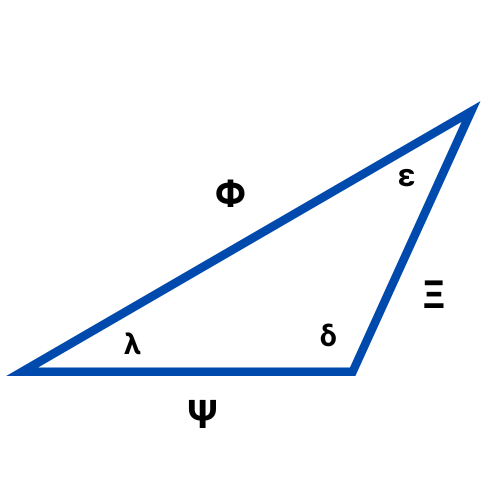
Law of sines

The law of sines states that

\begin{equation} \frac{\textnormal{Sin} \, (\lambda)}{\Xi} = \frac{\textnormal{Sin} \, (\epsilon)}{\Psi} = \frac{\textnormal{Sin} \, (\delta)}{\Phi} \end{equation}

Law of cosines

The law of cosines states that

\begin{equation} \Phi^2 = \Psi^2 + \Xi^2 - 2 \, \Psi \, \Xi \, \textnormal{cos} \, (\delta) \end{equation}

  Trigonometric functions  

Unit circle

Sine, cosine, tangent functions

Reciprocal trig functions

Inverse trig functions

The inverse trig functions are as follows

\begin{equation} \textnormal{Arcsine} \rightarrow \quad \textnormal{sin}^{-1} (न) = \eta \quad न \in [-1, 1] \end{equation} \begin{equation} \textnormal{Arccosine} \rightarrow \quad \textnormal{cos}^{-1} (ж) = \alpha \quad ж \in [-1, 1] \end{equation} \begin{equation} \textnormal{Arctangent} \rightarrow \quad \textnormal{tan}^{-1} (か) = \gamma \quad か \in [-\infty, \infty] \end{equation} \begin{equation} \textnormal{Arccosecant} \rightarrow \quad \textnormal{csc}^{-1} (未知) = \beta \end{equation} \begin{equation} \textnormal{Arcsecant} \rightarrow \quad \textnormal{sec}^{-1} (ي) = \theta \end{equation} \begin{equation} \textnormal{Arccotangent} \rightarrow \quad \textnormal{cot}^{-1} (ঞ) = \upsilon \end{equation}

Graphing trig functions

Symmetry and periodicity of trig functions

  Trigonometric identities  

Reciprocal and quotient

Pythagorean

Addition, subtraction, double-angle, half-angle

Cofunction

Symmetry and periodicity

Exercises

1. Verify DeMoivre's theorem for n = 3