Calculus 1
Derivatives
Derivatives and rates of change
Derivate as a function
Some functions have derivatives, and some do not.
Which functions have derivatives, and which do not?
Derivatives of polynomials and exponential functions
Power rule
Why does \( \frac{d}{dx} x^2 = 2x \, \)? We can think about this geometrically. Imagine \( x^2 \) as
an area. We increase the function, such that each side of the area grows. How many
sides grow? 2. Why does \( \frac{d}{dx} x^3 = 3x \)? We can also think about this geometrically.
Now it is the volume of a cube. Increase the function by a small amount, and each side of the cube grows.
How many sides of the cube are there?
Courtesy to 3blue1brown for help with this explanation!
Lets start with a general function, and represent the value of the function by the area of a shape. Lets use a square.
So if the value of the function is 7, the area of the square is 7, if the value of the function is 2, the area of the square is 2, etc.

Now, imagine we increase the value of the function with a corresponding
increase in the area of the square.

Lets just call this area Δf. So the total area is
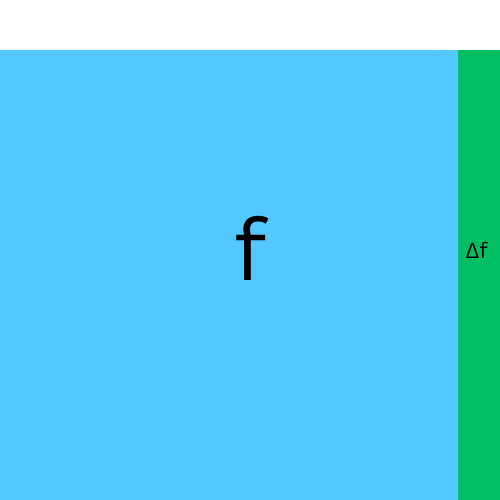
total area = f + Δ f.
A key point is that, for our function, let's say it's a function of x. So,

where the area changes based upon the input to f. So



It could be anything. Another key point is that,
how do we evaluate a change in the area when going from
f(a) to f(a + ε), where ε is a small number? So,
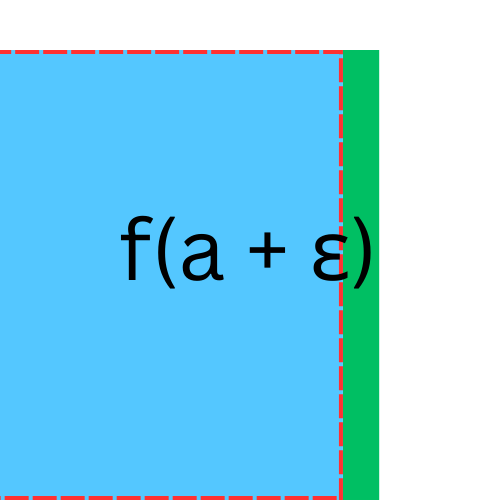
Or even

At this point our function could be anything,
\( \textnormal{sin}(x) \), \( 1 + 2x \), \( \frac{1}{i \, \textnormal{sin}(x)} \).
The point is that the geometric area is a visual representation of the value of
the function at certain value of x.
So what is the area of the change?
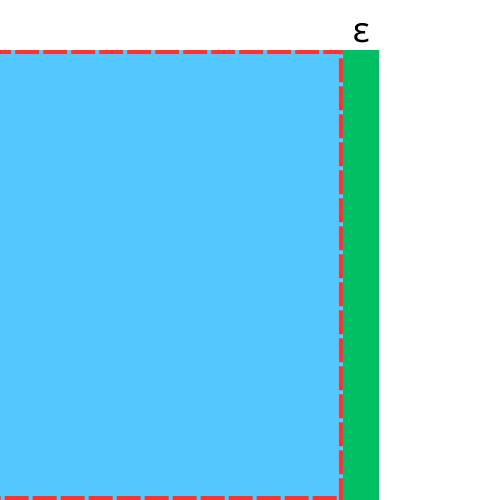
And what is the height?
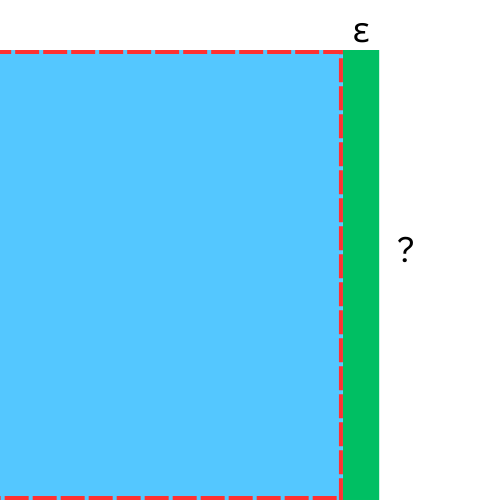
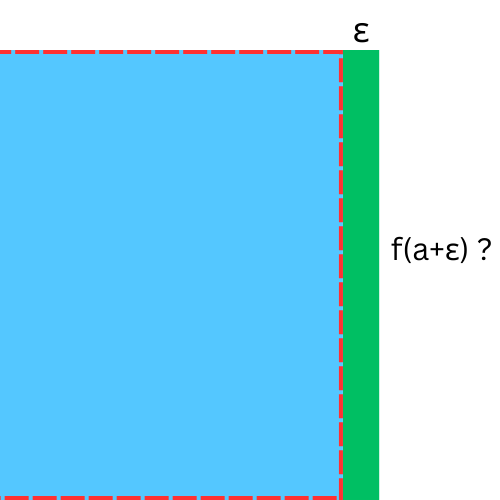
Or
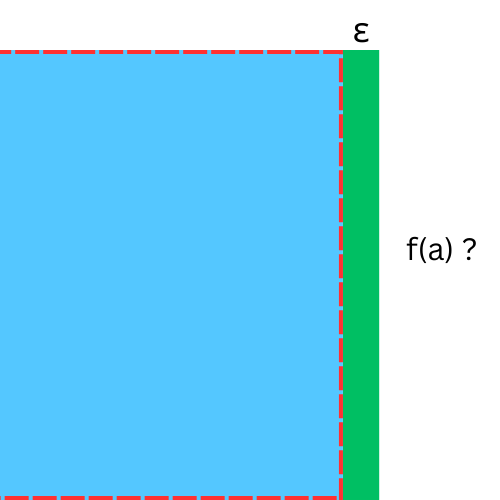
Or
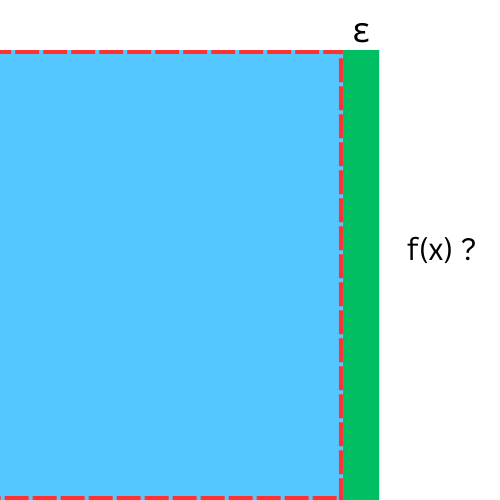
We will call it h. So
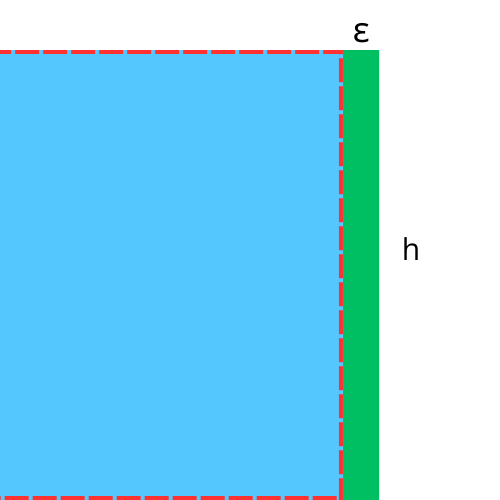
We know that area of a rectangle is base * height, so
Area of change = b h => \( \Delta f = ε * h \). So
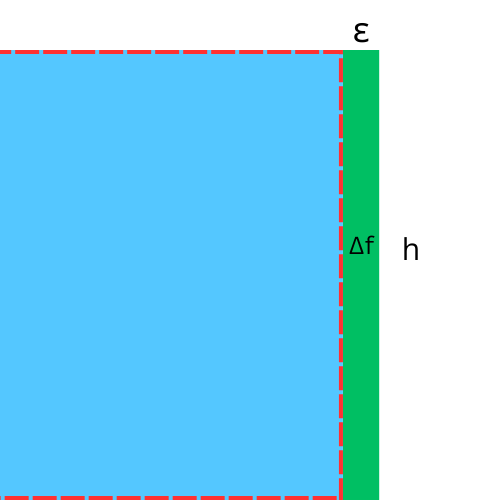
So \( h = \frac{\Delta f }{\epsilon } \)
And what is Δf ?
Well, Δf is the change in the value of the function, so
\( \Delta f = f(x + a) - f(x) \)
So geometrically this would be ...
Equations
\( \textnormal{lim}_{\, x \rightarrow a} \, f(x) = L \)
\( \frac{d}{dx} f(x) = \textnormal{lim}_{\, h \rightarrow 0} \, \frac{f(x + h) - f(x)}{(x + h) - x} \)
Derivative methods
\( \frac{d}{dx} (c x^n + d x^{n + 1} + b x^{n - 1} + p) = c \, n \, x^{n-1} + d(n + 1) x^n + b(n - 1)x^{n - 2} \)
The product and quotient rules
Derivatives of trigonometric functions
The chain rule
Implicit differentiation
Derivatives of logarithmic functions
Rates of change in the natural and social sciences
Exponential growth and decay
Related rates
Linear approximations and differentials
Hyperbolic functions















